
Parallel split coefficients are shown to be unnecessary for tests of common types.
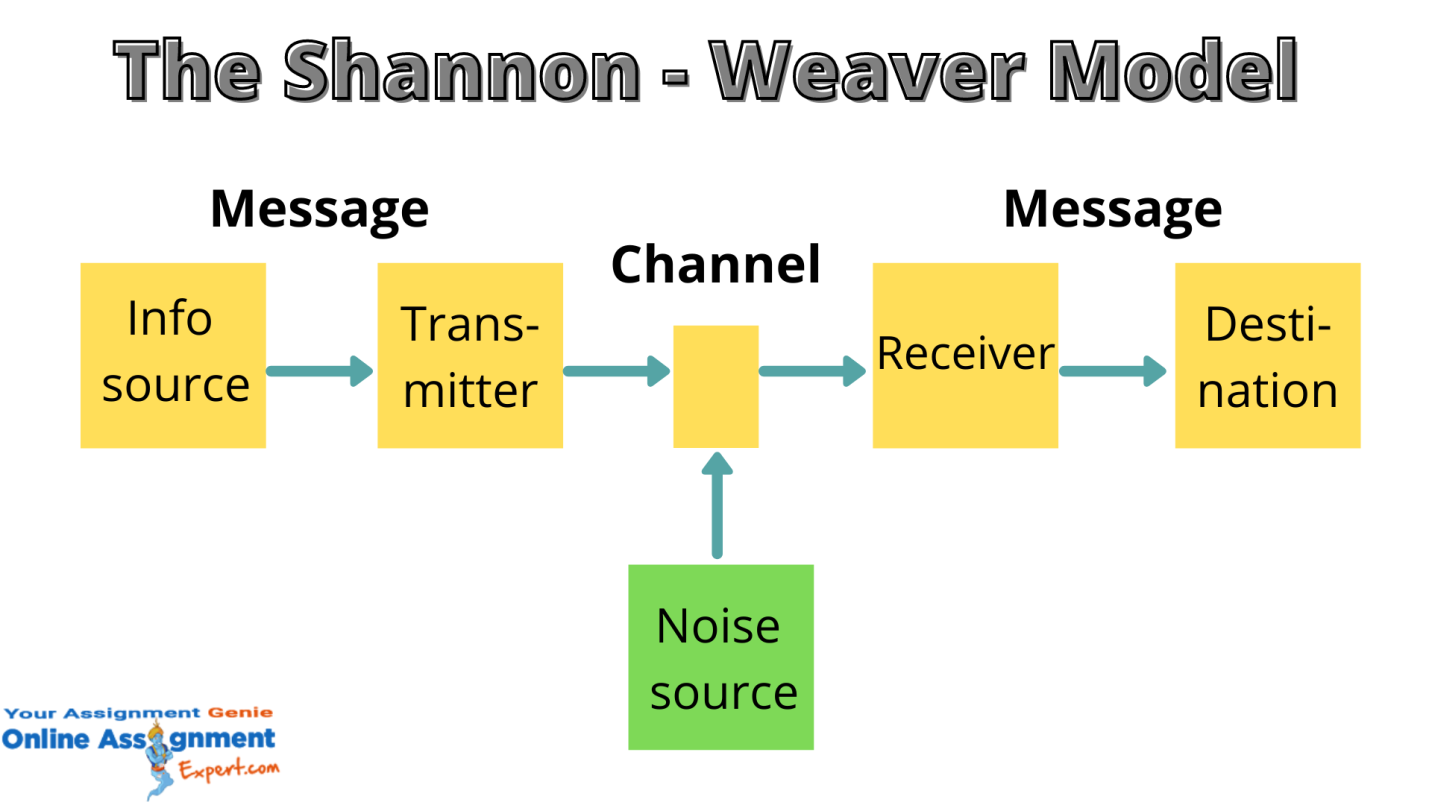

Comparison is made to the Guttman and Loevinger approaches. , derived from α, is shown to be an index of inter-item homogeneity. Tests divisible into distinct subtests should be so divided before using the formula. α is found to be an appropriate index of equivalence and, except for very short tests, of the first-factor concentration in the test. α is therefore an estimate of the correlation between two random samples of items from a universe of items like those in the test.
Abstract: A general formula (α) of which a special case is the Kuder-Richardson coefficient of equivalence is shown to be the mean of all split-half coefficients resulting from different splittings of a test.


 0 kommentar(er)
0 kommentar(er)
